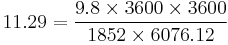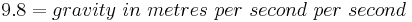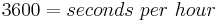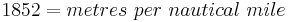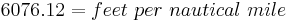ROT (aviation)

All aircraft must be able to perform a standard rate turn, also known as a rate one turn (ROT).

A standard rate turn for (light) airplanes is defined as a 3° per second turn, which completes a 360° turn in 2 minutes. This is known as a 2-minute turn, or rate one (= 180°/minute).
For heavy airplanes a standard rate turn is a 4-minute turn.

Instruments, either the turn and bank indicator or the turn coordinator, have the standard rate turn clearly marked. Light aircraft are equipped with 2-minute turn indicators while heavy aircraft are equipped with 4-minute turn indicators. This is very useful to pilots who are out of visual contact with the ground and for air traffic control when appropriate separation of aircraft is desired. The pilot banks the airplane such that the turn and slip indicator points to the standard rate turn mark and then uses a watch to time the turn. The pilot can pull out at any desired direction depending on the length of time in the turn.

A rate half turn (1.5° per second) is normally used when flying faster than 250 kt. The term rate two turn (6° per second) used on some low speed aircraft.

Angle of Bank formula

The formula for calculating the angle of bank for a specific True Airspeed (TAS) is:

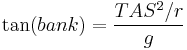
$\tan(bank)=\frac{TAS^2/r}{g}$

where $r$ is the radius of the turn and $g$ is the acceleration due to gravity. For a rate one turn and velocity in kt (nautical miles per hour), this comes to

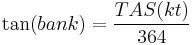$\tan(bank)=\frac{TAS(kt)}{364}$ .

A convenient approximation for the bank angle in degrees is

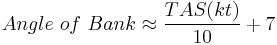
$Angle\ of\ Bank \approx \frac{TAS(kt)}{10} %2B 7$

Radius of Turn formula

One might also want to calculate the radius of a Rate 1,2 or 3 turn at a specific TAS.

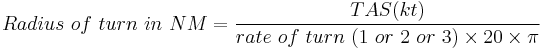
$Radius\ of\ turn\ in\ NM = \frac{TAS(kt)}{rate\ of\ turn\ (1\ or\ 2\ or\ 3) \times 20 \times \pi}$

or in SI units,

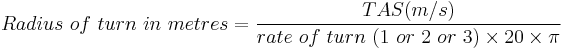
$Radius\ of\ turn\ in\ metres = \frac{TAS(m/s) }{rate\ of\ turn\ (1\ or\ 2\ or\ 3)\times 20 \times \pi}$

Use this formula to calculate the radius of turn in feet given velocity in knots and angle of bank:

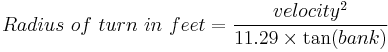
$Radius\ of\ turn\ in\ feet = \frac{velocity^2}{11.29 \times \tan(bank)}$

This is a simplified formula that ignores slip and returns zero for 90 degrees of bank.

The constant 11.29 is calculated:

$11.29 = \frac{9.8 \times 3600 \times 3600}{1852 \times 6076.12}$

$9.8 = gravity\ in\ metres\ per\ second\ per\ second$

$3600 = seconds\ per\ hour$

$1852 = metres\ per\ nautical\ mile$

$6076.12 = feet\ per\ nautical\ mile$